Статистические методы дают статистические ответы, а не аналитические оценки.
Линейная калибровка обычно считается простой, в особенности для высокоэффективной жидкостной хроматографии (ВЭЖХ). Ведь сам метод и правила не менялись уже на протяжении последних 20 лет (1).
Требования Международной конференции по гармонизации (ICH) (1) просты и хорошо известны:
- линейная зависимость должна быть оценена во всем диапазоне применения аналитической методики,
- линейность должна быть оценена путем визуального контроля графика сигналов как функции концентрации или содержания аналита,
- если существует линейная зависимость, то результаты испытания должны быть оценены с помощью соответствующих статистических методов, например, путем расчета линии регрессии методом наименьших квадратов по не менее чем пяти концентрациям, входящим в аналитический диапазон,
- данные самой линии регрессии могут быть полезны для получения математических оценок степени линейности:
- коэффициента корреляции,
- отрезка, отсекаемого на оси Y,
- наклона линии регрессии и остаточной суммы квадратов,
- также для оценки линейности может быть полезен анализ отклонения фактических точек данных от линии регрессии.
Требования ICH кажутся простыми. Просто проведите необходимые эксперименты, загрузите данные в статистический пакет или даже в Excel и выполните необходимые расчеты. Тем не менее, как же узнать действительно ли у вас прямая линия? В этом статье мы рассмотрим некоторые проблемы, допущения и ограничения регрессии обычным методом наименьших квадратов (OLS), проиллюстрированные с использованием экстраординарного набора данных.
Проблемы, допущения и ограничения регрессии OLS
Проблема № 1: доказательство того, что калибровка действительно является прямой линией. Однако это невозможно доказать. Проблема тянет свои корни из индуктивной статистики, в которой нулевая гипотеза состоит в том, что наша калибровка является прямой линией, однако подтвердить нулевую гипотезу невозможно. Все, что можно сделать, это показать, что альтернативная гипотеза (то есть, что наша калибровка по факту является кривой) маловероятна при заданной степени вероятности.
Проблема № 2: предположение о том, что чем больше значение коэффициента корреляции r2 то, тем лучше прямая линия. Утверждение «чем больше значение коэффициента корреляции r2» является ошибочным. r2 является мерой величины изменчивости, учитываемой моделью данных, а не линейностью. Эта истина не всегда осознается аналитическими химиками или сотрудниками отдела обеспечения качества (ОК), которые могут полагаться на r2.
| Таблица I: набор данных квартета Энскомба (2). | |||||||
| Квартет Энскомба | |||||||
| I | II | III | IV | ||||
| X | Y | X | Y | X | Y | X | Y |
| 10,0 | 8,04 | 10,0 | 9,14 | 10,0 | 7,46 | 8,0 | 6,58 |
| 8,0 | 6,95 | 8,0 | 8,14 | 8,0 | 6,77 | 8,0 | 5,76 |
| 13,0 | 7,58 | 13,0 | 8,74 | 13,0 | 12,74 | 8,0 | 7,71 |
| 9,0 | 8,81 | 9,0 | 8,77 | 9,0 | 7,11 | 8,0 | 8,84 |
| 11,0 | 8,33 | 11,0 | 9,26 | 11,0 | 7,81 | 8,0 | 8,47 |
| 14,0 | 9,96 | 14,0 | 8,10 | 14,0 | 8,84 | 8,0 | 7,04 |
| 6,0 | 7,24 | 6,0 | 6,13 | 6,0 | 6,08 | 8,0 | 5,25 |
| 4,0 | 4,26 | 4,0 | 3,10 | 4,0 | 5,39 | 19,0 | 12,50 |
| 12,0 | 10,84 | 12,0 | 9,13 | 12,0 | 8,15 | 8,0 | 5,56 |
| 7,0 | 4,82 | 7,0 | 7,26 | 7,0 | 6,42 | 8,0 | 7,91 |
| 5,0 | 5,68 | 5,0 | 4,74 | 5,0 | 5,73 | 8,0 | 6,89 |
Более 40 лет назад Энскомб написал статью, иллюстрирующую эту проблему на примере подражающих друг другу расчетным статистическим параметрам, в частности, r2 (2). Он показал таблицу из четырех наборов данных X, Y (таблица I), которые, после обработки методом регрессии OLS, дали одинаковые расчетные статистические параметры в пределах ошибки округления (таблица II).
| Таблица II: квартет Энскомба; некоторые расчетные статистические параметры (2). | |
| Уравнение регрессии | Y = 0,500 × X + 3,00 |
| Среднее значение X | 9,00 |
| Среднее значение Y | 7,50 |
| Sx/y | 1,237 |
| Коэффициент корреляции r2 | 0,666 |

Затем он показал графики четырех наборов данных (рисунок 1). Нетрудно заметить, что слепое следование расчетным параметрам не всегда является разумным.
Проблема № 3: модель OLS предполагает, что все ошибки содержаться в переменной Y (или отклике). Третья проблема является другим предположением, которое не всегда действительно или осознается. В ВЭЖХ переменная отклика (Y) обычно представляет собой площадь пика, а переменная X — концентрацию. Действительно ли концентрации не содержат ошибок?
Проблема № 4: остатки модели подчиняются нормальному распределению. Это предположение часто игнорируется, хотя ICH предлагает строить графики остатков. Остаток — это просто разность между полученным значением и значением, предсказанным регрессионной моделью. Оценка нормального распределения обычно относительно невысока, вследствие небольшого количества данных. Тем не менее, график нормальной вероятности можно легко построить с использованием стандартных статистических пакетов, например Minitab 17. В идеале все данные должны располагаться близко к центральной линии.
Возможно, это выглядит удивительно, что на графике остатков из квартета Энскомба только одна точка находится за пределами 95 % доверительного интервала (см. рисунок 2). Однако форма данных, подобная волне, должна вызвать подозрение и проведение дальнейшего исследования.

Проблема № 5: дисперсия постоянна во всем аналитическом диапазоне (требование гомоскедастичности). Это хорошее предположение при использовании количественных данных основных пиков с большими значениями функции отклика в ограниченном аналитическом диапазоне, например, от 80 % до 120 % от целевой концентрации. И это предположение может быть вполне разумным даже в больших диапазонах, например, от 20 % до 150 % от целевой концентрации. Однако для низких концентраций примесей, требующих калибровки от порога отчетности до 120 % от целевой концентрации, это предположение, вероятно, будет неверным, поэтому следует использовать альтернативные методы наименьших квадратов (например, метод взвешенных наименьших квадратов). Это должно быть очевидно, что статистические методы дают статистические ответы, а не аналитические оценки.
Пример
Один пользователь сети Minitab на LinkedIn опубликовал следующий пример набора данных линейности (3). Исходные данные представлены в таблице III. Стандартные растворы были приготовлены в шести концентрациях по три повтора каждой и охватывали диапазон концентраций от 0,004 мг/л до 0,030 мг/л, что составляло от 20 % до 150 % от целевой концентрации. График регрессии OLS представлен на рисунке 3.
| Таблица III: набор данных линейности с нормализованным откликом, недавно опубликованный в сети Minitab на LinkedIn | |||
| Концентрация раствора в % от целевой концентрации | Концентрация (мг/мл) | Площадь пика | Нормализованный отклик |
| 20% | 0,004 | 101030 | 25257500 |
| 20% | 0,004 | 100987 | 25246750 |
| 20% | 0,004 | 101663 | 25415750 |
| 30% | 0,006 | 148937 | 24822833 |
| 30% | 0,006 | 150090 | 25015000 |
| 30% | 0,006 | 150008 | 25001333 |
| 50% | 0,010 | 252579 | 25257900 |
| 50% | 0,010 | 252289 | 25228900 |
| 50% | 0,010 | 251375 | 25137500 |
| 80% | 0,016 | 417534 | 26095875 |
| 80% | 0,016 | 416060 | 26003750 |
| 80% | 0,016 | 417033 | 26064563 |
| 100% | 0,020 | 506341 | 25317050 |
| 100% | 0,020 | 506401 | 25320050 |
| 100% | 0,020 | 506959 | 25347950 |
| 150% | 0,030 | 762321 | 25410700 |
| 150% | 0,030 | 761557 | 25385233 |
| 150% | 0,030 | 761701 | 25390033 |
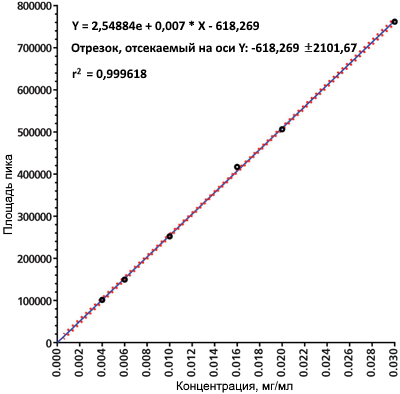
По этим данным видно, что r2 = 0,999618, а отрезок, отсекаемый на оси Y, неотличим от нуля с достоверностью 95 %. Как на счет достоверности для прямой линии? Впрочем, а как распределяются остатки (о чем спрашивал опубликовавший этот набор данных человек (см. рисунок 4)? Они определенно не подчиняются нормальному распределению, но почему?

Для начала давайте посмотрим на график остатков, предлагаемый ICH и показанный на рисунке 5. Совершенно ясно, что тут что-то непонятное с данными концентрации 0,016 %. Давайте предположим, что у нас есть доказательства того, что при приготовлении образцов с этой концентрацией была совершена ошибка, поэтому мы исключим её из анализа (рисунок 6). А теперь все в порядке?


По-видимому, исключение данных этой концентрации решило проблему, но есть ли еще чему поучиться? Давайте посмотрим на пересмотренные данные регрессии и их график (рисунок 7).

Видно, что наклон не сильно изменился, а r2 даже увеличился почти до единицы. Однако отрезок, отсекаемый на оси Y, должен быть и теперь уже более отрицательный, и значимо отличается от нуля. Отрезок, отсекаемый на оси Y, небольшой, приблизительно 0,4 % от отклика при 100 % от целевой концентрации, однако вероятность отрицательной площади пика при положительной концентрации должна насторожить хроматографистов.
Но помощь, как всегда, под рукой, поскольку существует полезный, но малоизвестный простой диагностический график, который не упоминается в ICH и известен как график чувствительности (4). Если площадь пика разделить на концентрацию (нормализованный отклик), то теоретически вы должны получить постоянное значение или, на практике, прямую линию, параллельную оси X, с небольшим случайным разбросом из-за шума измерения. Средним нормализованным откликом является наклон калибровочной линии. Если по данным из таблицы III построить графики чувствительности включая и исключая значения концентрации 0,016 %, то можно получить результаты, показанные на рисунке 8.

Ниже приведены три важные особенности, которые очевидно выражены на рисунке 8:
- нормализованные отклики не являются линейными,
- исключение данных концентрации 0,016 % просто сдвигает среднюю линию (наклон калибровочной кривой) немного вниз (приблизительно на 0,5 %),
- диапазон значений ниже концентрации 0,016 % намного больше, чем тот, что выше, что предполагает, что дисперсия не может быть постоянной во всем аналитическом диапазоне (пятая проблема). Статистическим термином для этого является гетероскедастичность (нарушение гомоскедастичности), когда величина дисперсии отличается во всем диапазоне значений независимой переменной, в данном случае концентрации.
Вывод
Статистические методы дают статистические ответы, а не аналитические оценки. Статистические инструменты, в данном случае линейная регрессия OLS, требуют разумной интерпретации результатов аналитиком, а не рабской приверженности статистической значимости параметров, в особенности r2. Всегда смотрите на данные и стройте графики чувствительности. Учитывая представленные в этой статье результаты, наиболее интересным было бы исследовать лабораторные записи для приведенного набора данных из примера для того, чтобы попытаться установить основную причину (-ы) наблюдаемых проблем с данными калибровки.
Литературные источники
- ICH, Q2(R1), Validation Of Analytical Procedures: Text And Methodology(ICH, Oct. 27, 1994, Nov. 6, 1996, incorporated November 2005).
- F. J. Anscome, American Statistician 27, 17-21 (1973).
- Gamal M. Mohamed, data set posted on the Minitab Network on LinkedIn, Feb. 12, 2015, www.linkedin.com/grp/post/166220-5970966595894288384.
- J. Ermer and P. Nethercote (Eds), Method Validation in Pharmaceutical Analysis, 2nd Edition, Section 5.5.1.2.1, p. 153 (Wiley-VCH, 2015).